Hack The Box: University Qualifiers 2021
Writing up some challenges from Hack The Box: University Qualifiers almost a month after it happened. I did 4+ challenges that I remember. Here they are.
Upgrades
This was an easy reversing challenge. Here the challenge description.

We are given a powerpoint named upgrades. We can decompress it:
We find there is a VBA macro inside it:

We open it with LibreOffice Present:
We see the following macro:
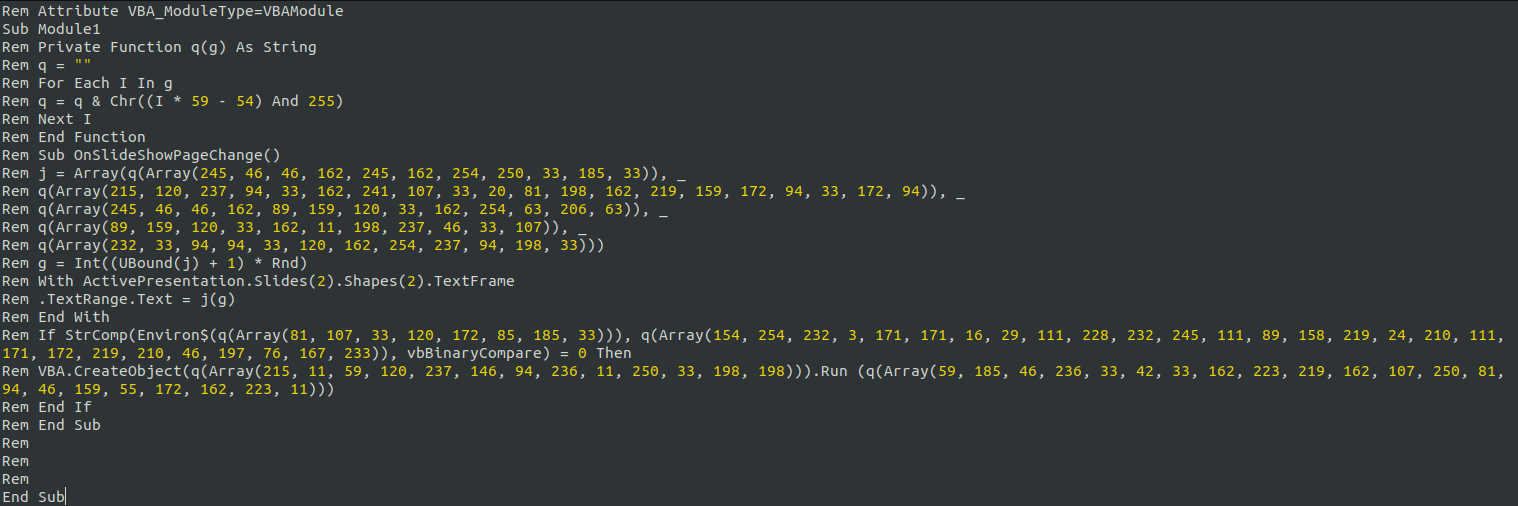
This is pretty easy to translate into python. We create copies of the arrays of ints too:
def q(s):
o = ""
for i in s:
o = o + chr((i * 59 - 54) & 255)
print(o)
return o
j = [245, 46, 46, 162, 245, 162, 254, 250, 33, 185, 33]
j1 = [215, 120, 237, 94, 33, 162, 241, 107, 33, 20, 81, 198, 162, 219, 159, 172, 94, 33, 172, 94]
j2 = [245, 46, 46, 162, 89, 159, 120, 33, 162, 254, 63, 206, 63]
j3 = [89, 159, 120, 33, 162, 11, 198, 237, 46, 33, 107]
j4 = [232, 33, 94, 94, 33, 120, 162, 254, 237, 94, 198, 33]
j5 = [81, 107, 33, 120, 172, 85, 185, 33]
j6 = [154, 254, 232, 3, 171, 171, 16, 29, 111, 228, 232, 245, 111, 89, 158, 219, 24, 210, 111, 171, 172, 219, 210, 46, 197, 76, 167, 233]
j7 = [215, 11, 59, 120, 237, 146, 94, 236, 11, 250, 33, 198, 198]
j8 = [59, 185, 46, 236, 33, 42, 33, 162, 223, 219, 162, 107, 250, 81, 94, 46, 159, 55, 172, 162, 223, 11]
q(j)
q(j1)
q(j2)
q(j3)
q(j4)
q(j5)
q(j6)
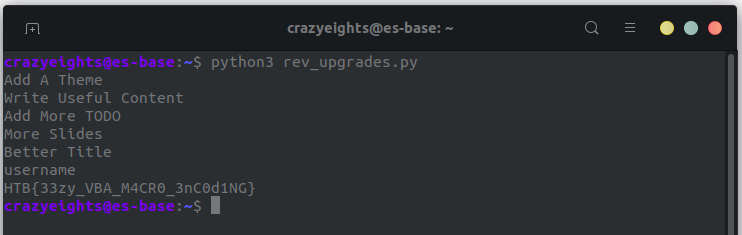
When we run it we get the flag:
Strike Back
This was an easy forensics challenge. It can be solved in only 1 step, if you avoid the rabbit hole:

We are given the following files:
The pcap file is a rabbit hole, you will find lots of different info. inside it, but nothing useful.
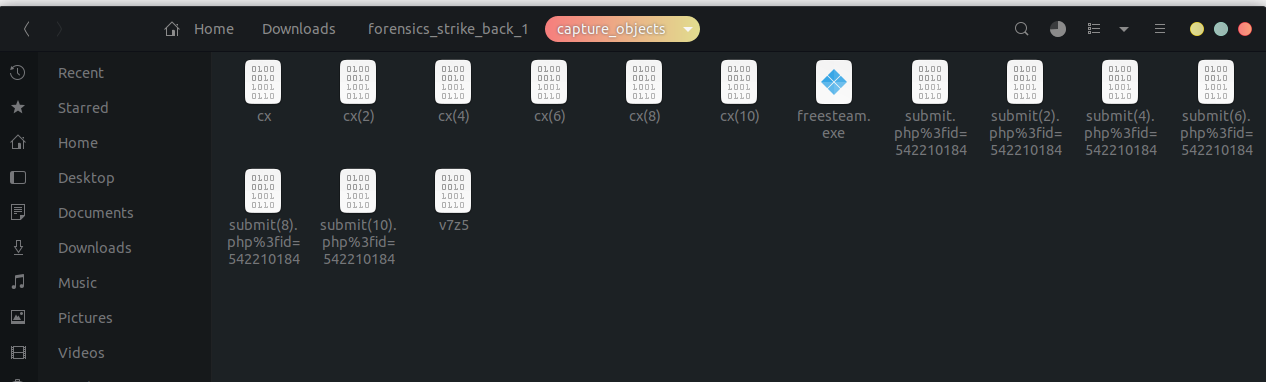
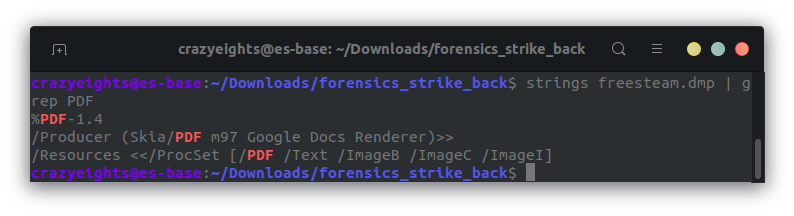
We focus on the .dmp file. Inside this file we find a PDF:
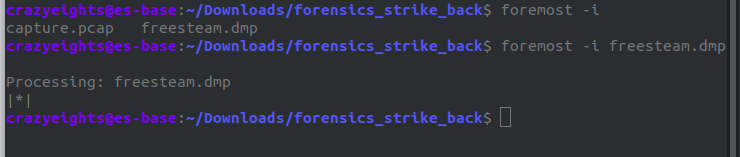
We use foremost to extract it:
We find the following files:
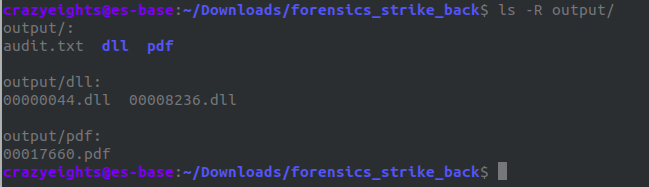
We open the PDF and find the flag:

Peel back the layers:
This challenge was another easy forensics challenge, it involved docker. Below is the challenge description.

For this challenge we use the container-diff tool:
https://github.com/GoogleContainerTools/container-diff
container-diff is a tool for analyzing and comparing container images.
First we pull the image:
docker pull steammaintainer/gearrepairimage
We get basic info. about the image:
docker inspect steammaintainer/gearrepairimage
docker version steammaintainer/gearrepairimage
docker image historty steammaintainer/gearrepairimage
docker image history steammaintainer/gearrepairimage
docker image history --no-trunc steammaintainer/gearrepairimage
docker save steammaintainer/gearrepairimage > image.tar
These commands extract a summary of modifications (source: hacktricks.xyz - Docker Forensics). We obviously want to find out info about the image layers (b/c the challenge name is Peeling back the layers).
chmod a+x container-diff-linux-amd64
./container-diff-linux-amd64 analyze -t history image.tar
./container-diff-linux-amd64 analyze -t sizelayer image.tar
./container-diff-linux-amd64 analyze -t metadata image.tar
We now have a bunch of different layers.
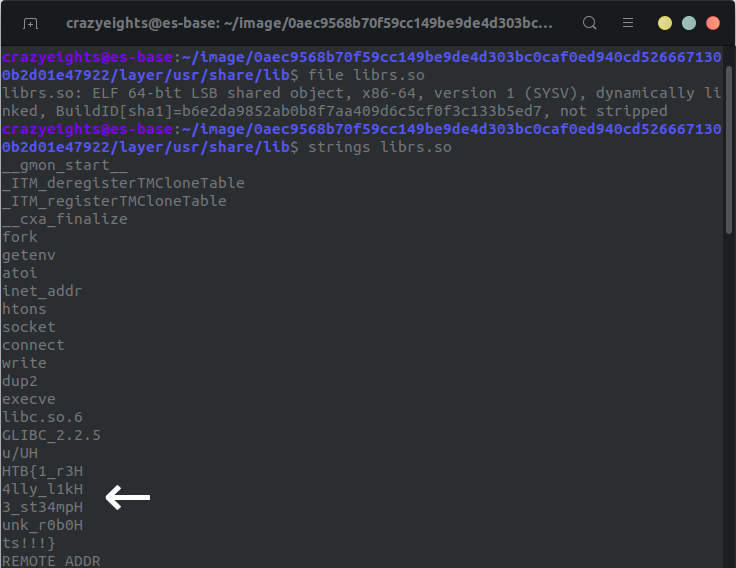
If we look around a bit we find a layer with the directory usr/share/lib, and the binary librs.so inside:
cd image/
cd 0aec9568b70f59cc149be9de4d303bc0caf0ed940cd5266671300b2d01e47922/
cd layer/
ls
cd usr/share/lib/
We run strings on the binary and find the flag:
Insane Bolt:
This challenge was a misc challenge that was easy ? - I hope not… Here is the challenge description.

Since I have almost no screenshots of the challenge I will do my best to describe it.
We were a robot, and we had to navigate through a maze, and get a diamond. If we didn’t pick the shortest path through the maze, we failed. We had to navigate through 500 different unknown mazes, and collect 500 diamonds to get the flag.
Here is an example maze:

Obviously the best way to solve this would be to use the A* search algorithm. We had to implement that from scratch for a project last year. I decided to use that. I used ptrlib to communicate with the socket.
import numpy as np
#---------------------------------
# Node Data Struct
# Holds all the information about a grid square
#---------------------------------
class Node:
def __init__(self, g, h, x, y):
# for simplicity g when the node n is visited g(n) is updated to g(n) + cost(s,n'), where n is a successor to n'
self.g = g
self.h = h
self.x = x
self.y = y
self.parent = None
# f(n) = g(n) + h(n)
def fn(self):
return self.g + self.h
# return the coordinates as a tuple
def _xy(self):return (self.x, self.y)
# equivalence checking => for the priority queue implementation
def __lt__(self, other):return self.fn() < other.fn()
def __le__(self, other):return self.fn() <= other.fn()
def __eq__(self, other):return self.fn() == other.fn()
def __ne__(self, other):return self.fn() != other.fn()
def __gt__(self, other):return self.fn() > other.fn()
def __ge__(self, other):return self.fn() >= other.fn()
# Show node as string
def __str__(self): return "({}, {})".format(self.x, self.y)
def __repr__(self): return str(self)
#----------------------
# Priority Queue Data Structure
#
# Uses numpy array operations for efficient placing of new nodes into the queue
#
# IN: s - first node in the queue
class PrQ:
def __init__(self, s):
self.front = np.empty(1, dtype=object)
self.front[0]=s
# _push - add node to the queue
# IN: n - new node to add
# pc - the cost from the start node to the current node
def _push(self, n, pc):
n.g = n.g + pc
# Find the node in the list that the new node would be placed in front of
# If the list is empty place the new node at the front
l = np.nonzero(self.front>n)[0]
if len(l) == 0:
self.front = np.append(self.front, n)
else:
self.front = np.insert(self.front, l[0], n)
# Pop the first node from the queue
def _pop(self):
if self.front.size == 0:
return None
h = self.front[0]
self.front = self.front[1:]
return h
# An Abstract Representation of the graph/grid
# IN:
# l - length of grid, w - width of grid
class AbGraph:
def __init__(self, l, w):
# Init Variables
self.grid = []
self.l = l
self.w = w
# start and end nodes
self.start_node = None
self.goal_nodes = []
self.min_cost = np.inf #min cost of a grid square for calculating heurisitic
# algorithm variables
self.path_cost = 0
self.explored = [] # store explored (expanded) nodes to be returned and written to file
self.optimal_path = []
self.visited_str = [] # store visited nodes (ie. nodes in the priority queue) so they are not added multiple times
# Build the grid of Nodes
# IN: gs - 2D array of strings (cost, S, X, or G)
def initialize_graph(self, gs):
c = {"S": 0, "G": 0, "X": "X"}
for i in range(self.l):
self.grid.append([])
for j in range(self.w):
# Create Node object for tile, with h(n) = inf because it hasn't been calculated yet
self.grid[i].append(Node(c.get(gs[i][j], gs[i][j]), np.inf, i, j))
# Store start and goal nodes
if gs[i][j] == "S":
self.start_node = self.grid[i][j]
elif gs[i][j] == "G":
self.goal_nodes.append(self.grid[i][j]._xy())
# Find min cost for heuristic function
elif gs[i][j]!="X" and float(gs[i][j]) < self.min_cost:
self.min_cost = float(gs[i][j])
self.start_node.h = 0
# Manhattan Distance
# IN: n - a node, g - a goal node
def md(self, n, g):
return abs(n[0] - g[0])+abs(n[1]-g[1])
# Calculate the heuristic for a node
# Since there is no reasoning behind the cost of the terrain, we must use the smallest cost for traveling between squares to prevent overestimating the cost
def heuristic(self, n):
return min([self.min_cost*self.md(n, g) for g in self.goal_nodes])
# Calculate the heuristic for all nodes in the grid (except for the wall nodes)
def calculate_heuristic(self):
for i in range(self.l):
for j in range(self.w):
if self.grid[i][j].g != "X":
self.grid[i][j].g = float(self.grid[i][j].g)
self.grid[i][j].h = self.heuristic(self.grid[i][j]._xy())
# Add neighbors
# IN: n - neighbor array to add nodes to
# x,y - location of node to find neighbors for
# p - the node to find neighbors for - to set as parent for new nodes found
def add_neighor(self, n, x, y, p):
# Check that neighboring location is in bounds of the grid
oob_x = {-1, self.l}
oob_y = {-1, self.w}
if x in oob_x or y in oob_y: return n
# Check location is not a wall
if type(self.grid[x][y].g) == str and self.grid[x][y].g == "X": return n
# Check location has not already been visited
if str(self.grid[x][y]) in self.visited_str: return n
# Add the neighboring node the list of neighbors, set its parent to p
self.grid[x][y].parent = p
n.append(self.grid[x][y])
self.visited_str.append(str(self.grid[x][y]))
return n
# Calculate the neighborhood of a particular node
def calculate_neighborhood(self, x, y, p):
neigh = []
neigh = self.add_neighor(neigh, x, y-1,p)
neigh = self.add_neighor(neigh, x, y+1,p)
neigh = self.add_neighor(neigh, x-1, y,p)
neigh = self.add_neighor(neigh, x+1, y,p)
return neigh
# Run the A* Search algorithm
# IN: gs - 2D array of strings representing grid
def run(self, gs):
self.initialize_graph(gs)
self.calculate_heuristic()
pr = PrQ(self.start_node)
self.visited_str.append(str(self.start_node))
while(True):
v = pr._pop()
# No path is found
if v is None:
print("No path found.")
return None, None, None
x = v.x
y = v.y
self.explored.append(v)
# Stop search, goal node has been reached
if v._xy() in self.goal_nodes:
break
# store the cost of the path from S to v
self.path_cost=v.g
neigh = self.calculate_neighborhood(x, y, v)
# Add the new nodes to the frontier priority queue
[pr._push(n, self.path_cost) for n in neigh]
self.trace_optimal_path(v)
return self.path_cost, self.explored, self.optimal_path
# From the goal node trace the path back to the start node
# IN: gn - goal node
def trace_optimal_path(self, gn):
node = gn
while node:
self.optimal_path = [node._xy()] + self.optimal_path
node = node.parent
# translate the shortest path the directional instructions (ie. L - left, R - right, D - down)
def optimal_path_to_string(path):
path_string = ""
for i in range(1, len(path)):
c1 = path[i-1]
c2 = path[i]
if c1[1] > c2[1]:
path_string+="L"
elif c1[1] < c2[1]:
path_string+="R"
else:
path_string+="D"
return path_string
def pathfinding(grid):
l = len(grid)
w = len(grid[0])
g = AbGraph(l, w)
c, v, o = g.run(grid)
print(o)
return optimal_path_to_string(o)
# -------------------------------------------------------------------------------
from ptrlib import *
sock = Socket("167.172.51.173", 31476)
options = {
"🤖": "robot",
"🔥": "fire",
"☠️": "death",
"🔩": "screw",
"💎": "diamond"
}
indxs = {"robot": "S", "fire": "X", "death": "X", "screw": "1", "diamond": "G"}
m = ""
# Initial Menu:
while "2. Play" not in m:
m = sock.recvline()
if not type(m) is str:
m = m.decode("utf-8")
print(m)
# Select Play
sock.sendline("2")
l1= sock.recvline()
print(l1)
# Recieve and parse the new board/grid from the server:
def get_board():
b = " "
grid = []
while b!="":
b = sock.recvline()
if not type(b) is str:
b = b.decode("utf-8")
print("debug1 "+b)
lines = b.split("\n")
for line in lines:
if line!='':
grid.append(line)
return grid
# get the board for the first round:
grid = get_board()
print(grid)
# use the A* algorithm to find the shortest path
# send the shortest path to the server
def play_round(lines):
board = []
for line in lines:
board.append([])
for s in line.split():
sym = options[s]
board[-1].append(indxs[sym])
print(board)
op = pathfinding(board)
print(op)
sock.sendline(op)
r = 0
while r < 500:
play_round(grid)
resp = sock.recvline().decode("utf-8")
resp += sock.recvline().decode("utf-8")
resp += sock.recvline().decode("utf-8")
print(resp)
if "[-] Wrong answer or time limit exceeded!" in resp:
break
if "Congratulations! This is your reward!" in resp:
break
grid = get_board()
r+=1
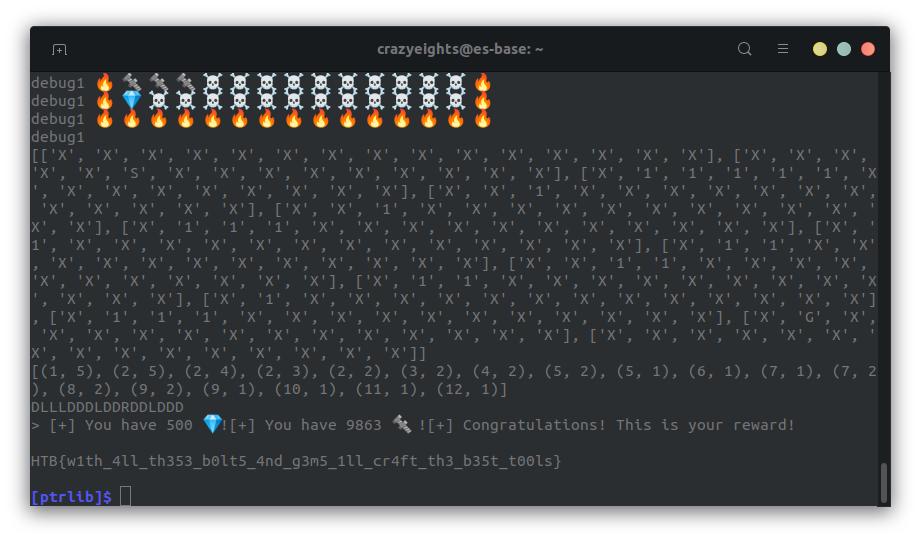
Here we see the flag (along with alot of debugging ;) )
FIN. This CTF was fun, but I had 2 assignments, and a test the week after, and I had to split my time, I wish I could have done more of it.. :(