CTFlearn: rsa_noob

The rsa_noob challenge from CTFlearn is an medium crypto challenge. Crypto is not my strongest area, so this was a good entry level challenge.

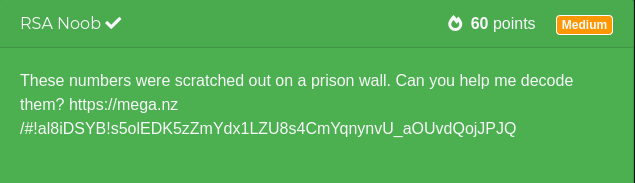
Download he file rsa_noob.txt from mega.nz. Inside is the following text:

e: 1
c:9327565722767258308650643213344542404592011161659991421
n: 245841236512478852752909734912575581815967630033049838269083

Since I took a crypto course last term I probably should remember what those meant. I didn’t and had to look it up.

c = ciphertext
m = messsage
p,q - primes

This is from my notes:

When e = 1 then d is also equal to 1 because d*e = 1*mod(tot(n)), so d = 1*mod(tot(n))

where:

tot(n) = (p-1)*(q-1)

Since we know d=1 and since c^1 = c then we can just convert the c integer to a byte string.

c contains some number of bytes, as the message is a byte stream/array (8-bit octets) encoded to an integer. When the message was encoded the array was looped over and each byte was OR-ed into a successively higher location in the output integer.

We can reverse this operation by doing the following (found on stackoverflow):

e = 1
c = 9327565722767258308650643213344542404592011161659991421
n = 245841236512478852752909734912575581815967630033049838269083

def integer_to_bytes(integer, _bytes):
    output = bytearray()
    for byte in range(_bytes):        
        output.append((integer >> (8 * (_bytes - 1 - byte))) & 255)
    return output

#print(len(str(c))) <- 55
print(integer_to_bytes(c, 54))

The function integer_to_bytes expects to extract _bytes bytes from integer. It repeatedly applies the bitmask 255 to integer to obtain the lowest 8 bits, and adds these bits to the output, then shifts integer right 8 bits.

Note that we don’t need to use e, or n.

When we run this code we get:

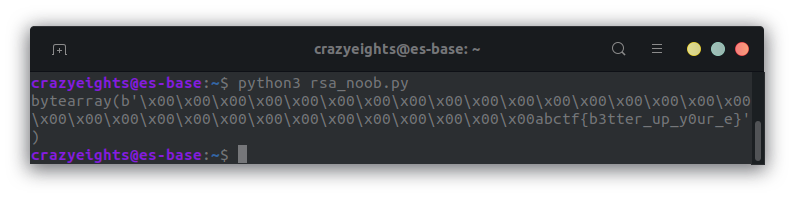
We can see the flag at the end of the byte array.

FIN. 🥳